Credit For The Image : theengineeringprojects.com
Numerical is at last
Unit 1: Fundamentals of Fluids
Unit 1: Fundamentals of Fluids -
1.1 Definition, Scope, and Application in Civil Engineering
Fluid mechanics is a fundamental branch of physics and engineering that deals with the behavior of fluids, which include both liquids and gases. In civil engineering, understanding fluid mechanics is essential because it plays a significant role in various aspects of design and analysis. Here's an overview of the definition, scope, and applications of fluid mechanics in civil engineering:
1.1.1 Definition of Fluid Mechanics:
Fluid mechanics is the study of fluids in motion and at rest. It focuses on the principles that govern the behavior of fluids, including the forces that act upon them, their flow patterns, and how they interact with solid surfaces. Fluid mechanics is a branch of continuum mechanics and is divided into two main branches:
- Fluid statics: The study of fluids at rest, where the fluid is in equilibrium, and there is no relative motion between different parts of the fluid.
- Fluid dynamics: The study of fluids in motion, including the analysis of forces, pressures, and velocity distributions in moving fluids.
1.1.2 Scope of Fluid Mechanics in Civil Engineering:
Fluid mechanics is an essential field in civil engineering, as it is relevant to various areas and applications, including but not limited to:
a. Hydraulics: Hydraulics is the branch of fluid mechanics that deals with the behavior of water and other liquids. It is crucial in the design and analysis of water supply systems, drainage systems, sewage systems, and irrigation systems.
b. Hydrology: Hydrology is the study of water resources, including rainfall, surface water, groundwater, and their interactions. It is essential for designing flood control measures, water resource management, and environmental impact assessments.
c. Fluid Transport: Fluid mechanics is vital in designing pipelines, pumps, and channels for the transportation of fluids like water, oil, and natural gas.
d. Environmental Engineering: Understanding fluid mechanics is necessary for designing wastewater treatment plants, stormwater management systems, and pollution control measures.
e. Structural Engineering: Fluid forces, such as wind and water pressure, can have a significant impact on the design and stability of buildings and structures.
f. Geotechnical Engineering: Fluid mechanics plays a role in soil mechanics, as the behavior of water in soils affects the stability and settlement of foundations and embankments.
1.1.3 Applications in Civil Engineering:
Fluid mechanics finds applications in various aspects of civil engineering, including:
- Designing and analyzing water distribution networks.
- Calculating flow rates and pressures in sewer systems.
- Modeling and predicting river and coastal erosion.
- Assessing the stability of dams and levees.
- Analyzing the effects of wind loads on buildings and structures.
- Designing efficient drainage systems.
- Evaluating the impact of groundwater flow on excavations and tunnels.
- Understanding the behavior of fluids in soil and rock formations during geotechnical investigations.
In conclusion, fluid mechanics is a fundamental discipline in civil engineering, as it provides the foundation for addressing critical issues related to the flow and behavior of fluids in various engineering applications. A solid understanding of fluid mechanics is crucial for civil engineers to design, analyze, and manage systems that involve the movement and behavior of fluids in our built environment.
1.2 Control Volume and Continuum Concept
1.2.1 Control Volume:
In the study of fluid mechanics, a control volume is a fundamental concept used to analyze and understand the behavior of fluids. It is a specific region in space that is chosen for analysis, and it can be fixed or moving. The control volume is an essential concept because it allows engineers and scientists to focus on a specific area of interest, such as a section of a pipe, a turbine, or a portion of a river, to analyze the flow of fluids in and out of that region.
The key characteristics of a control volume are as follows:
- Control Surface: The boundary that defines the control volume is known as the control surface. It can be a physical boundary, an imaginary boundary, or even a combination of both. Fluid can flow in and out of the control volume through this boundary.
- Mass Flow In and Out: Fluid can enter or leave the control volume, and these mass flow rates are typically considered to analyze how mass is conserved within the region.
- Energy Flow In and Out: Energy can also enter or leave the control volume through heat transfer or mechanical work. The analysis of energy flow is essential for understanding the behavior of fluids, such as in turbines or heat exchangers.
- Momentum Transfer: The control volume concept is used to analyze the momentum transfer between the fluid and the control volume. This is crucial for understanding the forces acting on the control volume and the resulting motion of the fluid.
Control volumes are used to apply the fundamental principles of fluid mechanics, such as the conservation of mass, energy, and momentum, within a specific region of interest. This enables engineers to design and analyze a wide range of devices and systems, from pumps and turbines to heat exchangers and pipelines.
1.2.2 Continuum Concept:
The continuum concept is another fundamental idea in fluid mechanics. It assumes that matter is continuous and that there are no voids or gaps at the microscopic level. In other words, the continuum concept treats a fluid as a continuous substance without considering its molecular structure. This assumption is generally valid for most practical engineering problems and is crucial for simplifying the analysis of fluid behavior.
Key aspects of the continuum concept include:
- Continuity Equation: The continuum concept is employed in the development of the continuity equation, which expresses the conservation of mass within a fluid as a continuous medium.
- Constitutive Equations: The behavior of the fluid, including its viscosity, density, and other properties, is described using constitutive equations that are derived based on the continuum assumption.
- Simplified Modeling: Treating fluids as continuous media simplifies the mathematical modeling of fluid flow and allows for the use of partial differential equations, such as the Navier-Stokes equations, to describe fluid behavior.
The continuum concept is valid as long as the characteristic length scales of the problem are significantly larger than the mean free path of the fluid molecules. In most civil engineering applications, such as designing water distribution systems, modeling river flow, or analyzing air flow around buildings, the continuum assumption is entirely appropriate and simplifies the analysis and design process.
In summary, the control volume and continuum concept are fundamental to the study of fluid mechanics in civil engineering. Control volumes enable engineers to focus on specific regions of interest for analysis, while the continuum concept simplifies the treatment of fluids as continuous media, making it easier to model and analyze their behavior. These concepts are essential for designing and understanding various fluid systems in civil engineering applications.
1.3 Fluid Properties
Understanding the properties of fluids is crucial in fluid mechanics and civil engineering. Here are some of the key fluid properties:
1. Mass Density (ρ):
Mass density, often denoted as ρ, is the measure of the mass of a fluid per unit volume. It is expressed in units such as kilograms per cubic meter (kg/m³) for the SI system. Mass density is a fundamental property of a fluid and is important in the context of fluid mechanics because it affects the behavior of fluids under the influence of external forces, such as gravity.
2. Specific Weight (γ):
Specific weight, denoted as γ, is the weight per unit volume of a fluid. It is related to mass density and the acceleration due to gravity (g) as γ = ρ * g. The unit of specific weight is typically newtons per cubic meter (N/m³) in the SI system. Specific weight is useful for analyzing fluid statics problems, particularly for calculating pressure variations in fluids.
3. Specific Gravity (SG):
Specific gravity is a dimensionless quantity that compares the density of a fluid to the density of a reference substance, usually water. It is calculated as the ratio of the fluid's density to the density of water (ρ_fluid / ρ_water). Specific gravity is often used to classify and identify different fluids, such as liquids, by their relative density.
4. Cavitation:
Cavitation occurs when the pressure of a fluid drops below the vapor pressure, causing the formation of vapor or gas bubbles within the fluid. These bubbles can collapse and create significant damage to surfaces in contact with the fluid. In civil engineering, cavitation can be a concern in hydraulic systems, pumps, and propellers, where it can lead to erosion and reduced efficiency.
5. Vapor Pressure:
Vapor pressure is the pressure exerted by the vapor phase of a liquid when it is in equilibrium with its liquid phase at a given temperature. It is a function of temperature and varies with different liquids. Understanding vapor pressure is important for applications involving the boiling and condensation of liquids, such as in steam systems or distillation processes.
6. Surface Tension:
Surface tension is a property of the surface of a liquid that results in the surface behaving like a stretched elastic membrane. It is due to the cohesive forces between molecules at the surface. Surface tension has applications in civil engineering, such as in the behavior of capillary rise in soil and the stability of free water surfaces.
7. Capillarity:
Capillarity refers to the ability of a fluid to flow in narrow spaces or capillary tubes against the force of gravity. It is influenced by surface tension and the wetting properties of the fluid and the solid surfaces. Capillarity is important in soil mechanics, as it affects the rise of water in soils and the stability of foundations.
8. Viscosity:
Viscosity is a measure of a fluid's resistance to flow. It quantifies the internal friction within the fluid as adjacent layers of fluid move relative to each other. Viscosity is a critical property in civil engineering, especially in applications involving fluid flow and transportation, such as designing pipelines, pumps, and hydraulic systems.
1.4.1 Types of Fluid Pressure:
Fluid pressure is the force per unit area exerted by a fluid on its surroundings. There are several types of fluid pressure, each with its unique characteristics:
a. Hydrostatic Pressure: Hydrostatic pressure is the pressure exerted by a fluid at rest due to the weight of the fluid above it. It increases with depth and is described by Pascal's law. The hydrostatic pressure is given by the formula P = ρ * g * h, where P is pressure, ρ is fluid density, g is the acceleration due to gravity, and h is the depth of the fluid.
b. Dynamic Pressure: Dynamic pressure is associated with the motion of a fluid and is a measure of the kinetic energy of the fluid particles. It plays a significant role in fluid flow, especially in applications like aerodynamics and fluid transport systems. Dynamic pressure is given by the formula P = 0.5 * ρ * V^2, where P is pressure, ρ is fluid density, and V is the velocity of the fluid.
c. Total Pressure: Total pressure is the sum of the hydrostatic pressure and dynamic pressure at a given point in a fluid. It represents the total energy at that point and is crucial in applications involving fluid flow and energy transfer, such as in pumps and turbines.
d. Atmospheric Pressure: Atmospheric pressure is the pressure exerted by the Earth's atmosphere on the Earth's surface. It is typically measured using a barometer and varies with altitude. At sea level, standard atmospheric pressure is approximately 101.3 kPa or 1 atm.
1.4.2 Pressure Head:
Pressure head is a concept used to describe the potential energy of a fluid based on its pressure. It is particularly important in hydrodynamics and hydraulics. Pressure head is defined as the height to which a fluid could be raised by its own pressure, assuming no other external forces are acting on it. It is given by the formula h = P / (ρ * g), where h is the pressure head, P is the pressure, ρ is the fluid density, and g is the acceleration due to gravity.
Pressure head is useful for understanding how pressure differences affect fluid levels and flow in hydraulic systems. It's often used to describe the energy in fluid systems and is essential for the design and analysis of systems like water supply networks and pipelines.
1.4.3 Laws of Pressure:
Two fundamental laws that govern fluid pressure in various situations are:
a. Pascal's Law: Pascal's law, also known as Pascal's principle, states that when there is an external change in pressure applied to a confined fluid, that change is transmitted undiminished throughout the entire fluid. This law is the basis for hydraulic systems, where a small force applied to a small piston can create a larger force on a larger piston, allowing for the amplification of mechanical work.
b. Boyle's Law: Boyle's law relates the pressure and volume of a gas at constant temperature. It states that the pressure of a gas is inversely proportional to its volume, assuming the temperature remains constant. Mathematically, P1 * V1 = P2 * V2, where P1 and V1 are the initial pressure and volume, and P2 and V2 are the final pressure and volume.
These laws of pressure are fundamental in understanding and designing various fluid systems, whether in hydraulics, pneumatics, or the analysis of fluid behavior in civil engineering applications.
1.5 Measurement of Pressure: Manometers
Measuring fluid pressure is a fundamental aspect of fluid mechanics and engineering. Manometers are commonly used instruments to measure pressure in various applications. There are several types of manometers, including piezometers, U-tube manometers, and micro manometers. Let's explore these different types of manometers:
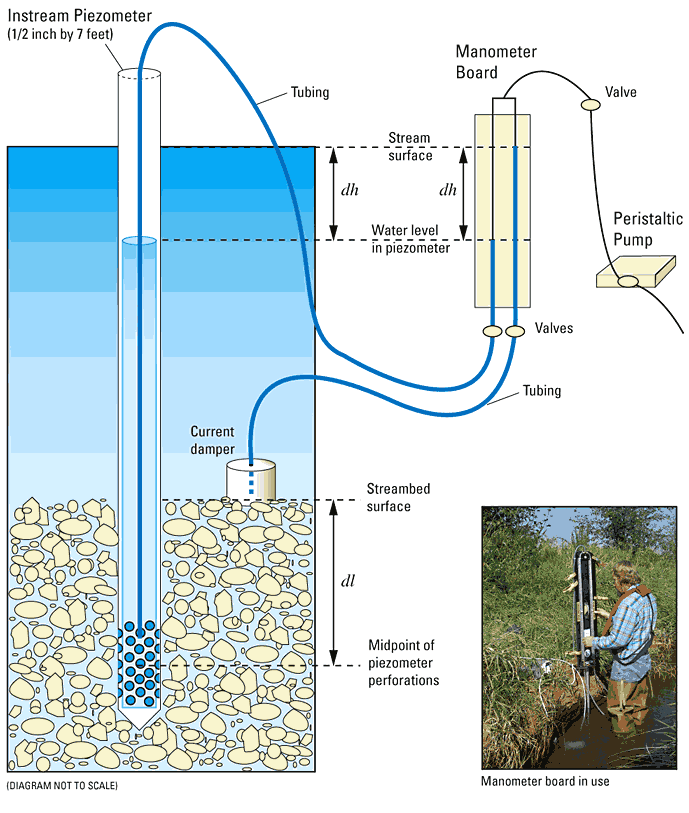
1.5.1 Piezometer:
Credit for image: pubs.usgs.gov
A piezometer is a simple and common device used to measure fluid pressure at a specific point in a fluid column. It typically consists of a vertical tube that is open at the top and connected to the fluid whose pressure is to be measured. The height of the fluid column in the piezometer indicates the pressure of the fluid at that point.
Key features of a piezometer:
- It provides a direct reading of the pressure at the point where it is inserted into the fluid.
- The pressure is determined by the height of the fluid column, and it is measured in units of length, such as meters or feet.
- Piezometers are suitable for measuring static pressures in open or closed systems, such as groundwater levels in wells or liquid levels in tanks.
1.5.2 U-Tube Manometer:
CREDIT FOR PHOTO byjus.com
A U-tube manometer is a more versatile and widely used device for measuring fluid pressure. It consists of a U-shaped tube partially filled with a dense manometric fluid, such as mercury, and an open end that is connected to the fluid whose pressure is being measured. The height difference between the two legs of the U-tube provides a measure of the pressure difference between the reference fluid (usually air) and the fluid being measured.
Key features of a U-tube manometer:
- It measures pressure differences (differential pressure) between two points in a system.
- The pressure difference is directly related to the height difference of the manometric fluid in the two legs of the U-tube.
- U-tube manometers are commonly used in applications like measuring pressure drops across filters, pumps, and control valves.
1.5.3 Micro Manometers: Credit for the image Science Direct.com
Micro manometers are precision instruments designed for accurate and sensitive pressure measurements. They are used to measure very low pressures and are often used in laboratory settings and industrial applications where high accuracy is required.
Key features of micro manometers:
- They are designed to measure very small pressure differences with high precision.
- Micro manometers may use various mechanisms, such as diaphragms, Bourdon tubes, or electronic sensors, to convert pressure into readable values.
- These instruments are commonly used in fields like aerodynamics, fluid dynamics research, and industries that require precise pressure measurements.
Manometers play a crucial role in civil engineering and various other engineering disciplines for measuring pressures in pipelines, hydraulic systems, water supply networks, and other fluid systems. The choice of a specific manometer type depends on the nature of the pressure being measured and the required accuracy of the measurement. Proper calibration and maintenance of manometers are essential to ensure accurate and reliable pressure readings.
NUMERICAL:
Example 1.3. A plate 0.05 mm distant from a fixed plate moves at 1.2 m/s and requires a force of 2.2 N/m² to maintain this speed. Find the viscosity of the fluid between the plates.
Solution,
dy=t=1.8 x 10^-3m
23.33 = µ x (0.36/1.8 x 10 ^ -3)
µ = (23.33 x 1.8 x 10 ^-3 /0.36 )
=1.66 N.S Per Meter Square
=11.66Poise
Leave your suggestion below in comment box and share it to friends if you think it is helpful and support me






Thanks for this notes really appricated
ReplyDeletePlease add more numericals
ReplyDelete